Nous reprenons ici le code du tutoriel Build natural language processing systems using TensorFlow qui s’appuie sur un jeu de données correspondant à des critiques de films (policiers) d’avant 2011.
Ces données sont réparties en 2 lots de 25 000 enregistrements (training/test).
Le but de l’exercice est de classer automatiquement un film à partir des commentaires apportés, en positif ou négatif.
Le code est présenté ici dans une version simplifiée.
Tout ce qui a déjà été commenté dans les tutoriels précédents est ignoré ici.
import tensorflow as tf
print(tf.__version__)
2.2.0
import tensorflow_datasets as tfds
imdb, info = tfds.load("imdb_reviews", with_info=True, as_supervised=True)
Downloading and preparing dataset imdb_reviews/plain_text/1.0.0 (download: 80.23 MiB, generated: Unknown size, total: 80.23 MiB) to /root/tensorflow_datasets/imdb_reviews/plain_text/1.0.0...
Dl Completed...: 100%
1/1 [00:09<00:00, 9.55s/ url]
Dl Size...: 100%
80/80 [00:09<00:00, 8.40 MiB/s]
import numpy as np
train_data, test_data = imdb['train'], imdb['test']
training_sentences = []
training_labels = []
testing_sentences = []
testing_labels = []
for s,l in train_data:
training_sentences.append(str(s.numpy()))
training_labels.append(l.numpy())
for s,l in test_data:
testing_sentences.append(str(s.numpy()))
testing_labels.append(l.numpy())
len(training_sentences)
25000
len(testing_sentences)
25000
training_labels_final = np.array(training_labels)
testing_labels_final = np.array(testing_labels)
Ce qu’on entend par embedding, c’est une matrice de poids qu’on peut indexer. Voir à ce sujet le cours fastai
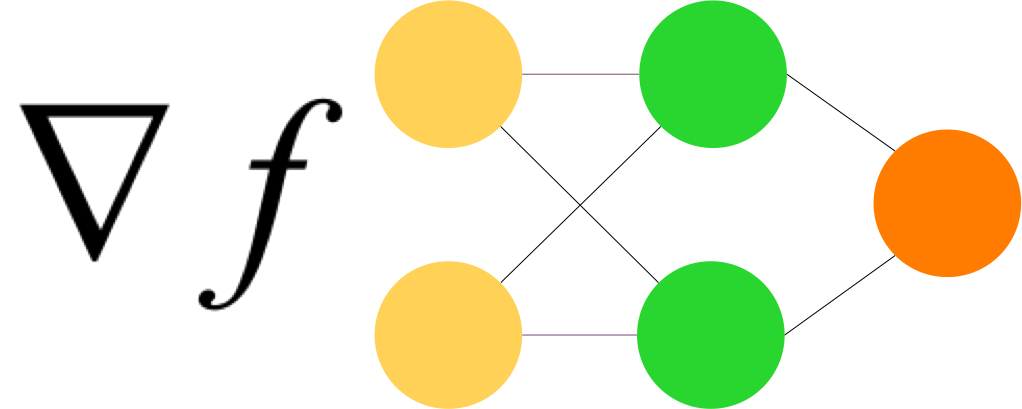
La dimension embedding_dim est arbitraire, ou plus exactement n’est pa définie par un calcul formel. Elle est arbitraire comme l’est le nombre de couches de neurones ou le nombre de neurones par couches. Ce n’est pas pour autant qu’elle doit être n’importe quoi !
Pour illustrer embedding, prenons un exemple de collaborative flitering.
Supposons que 5 cinéphiles aient noté des films (de f1 à f6).
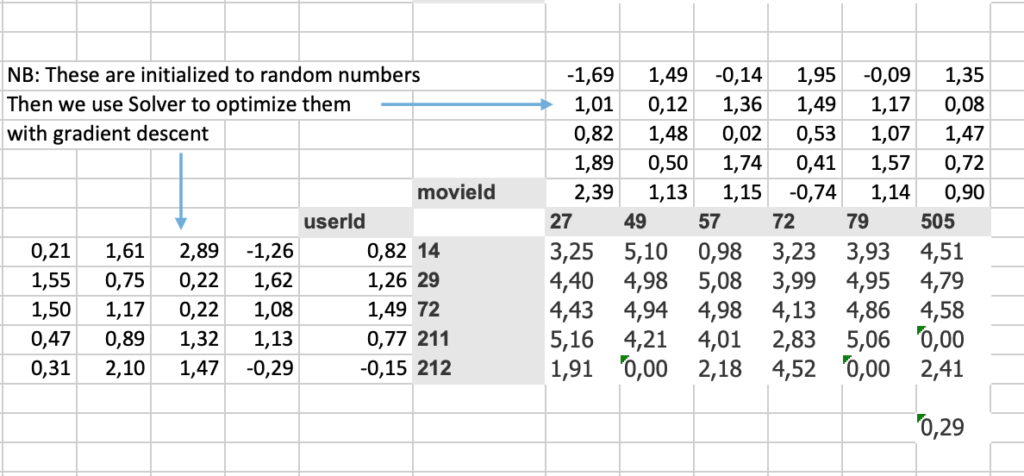
[table “1” not found /]Nous allons calculer 2 matrices (embeddings) qui permettent de prédire la note qui sera attribuée à un film.
Nous faisons un produit matriciel (un biais est aussi ajouté, mais ce n’est pas important à discuter ici) de ces deux matrices, initialisées de façon aléatoire, nous calculons le coût (0,29) et nous minimisons ce coût par descente du gradient (tout ça sous Excel).
Après quelques itérations, les résultats obtenus sont ceux de la matrice ci-dessous.
Nous utiliserons le même principe en NLP.
Mathematically speaking, embeddings generate word vectors and use those word vectors to pass to the future layers. We will use a parameter called ‘embedding_dim’ which is an integer.
https://mc.ai/a-complete-multi-class-text-classifier-step-by-step/
vocab_size = 10000
embedding_dim = 16
max_length = 120
trunc_type='post'
oov_tok = "<OOV>"
from tensorflow.keras.preprocessing.text import Tokenizer
from tensorflow.keras.preprocessing.sequence import pad_sequences
tokenizer = Tokenizer(num_words = vocab_size, oov_token=oov_tok)
tokenizer.fit_on_texts(training_sentences)
word_index = tokenizer.word_index
word_index = tokenizer.word_index
86539
sequences = tokenizer.texts_to_sequences(training_sentences)
padded = pad_sequences(sequences,maxlen=max_length, truncating=trunc_type)
testing_sequences = tokenizer.texts_to_sequences(testing_sentences)
testing_padded = pad_sequences(testing_sequences,maxlen=max_length)
model = tf.keras.Sequential([
tf.keras.layers.Embedding(vocab_size, embedding_dim, input_length=max_length),
tf.keras.layers.Flatten(),
tf.keras.layers.Dense(6, activation='relu'),
tf.keras.layers.Dense(1, activation='sigmoid')
])
model.compile(loss='binary_crossentropy',optimizer='adam',metrics=['accuracy'])
model.summary()
model = tf.keras.Sequential([
tf.keras.layers.Embedding(vocab_size, embedding_dim, input_length=max_length),
tf.keras.layers.Flatten(),
tf.keras.layers.Dense(6, activation='relu'),
tf.keras.layers.Dense(1, activation='sigmoid')
])
model.compile(loss='binary_crossentropy',optimizer='adam',metrics=['accuracy'])
model.summary()
Model: "sequential"
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
embedding (Embedding) (None, 120, 16) 160000
_________________________________________________________________
flatten (Flatten) (None, 1920) 0
_________________________________________________________________
dense (Dense) (None, 6) 11526
_________________________________________________________________
dense_1 (Dense) (None, 1) 7
=================================================================
Total params: 171,533
Trainable params: 171,533
Non-trainable params: 0
_________________________________________________________________
num_epochs = 10
model.fit(padded, training_labels_final, epochs=num_epochs, validation_data=(testing_padded, testing_labels_final))
Epoch 1/10
782/782 [==============================] - 5s 7ms/step - loss: 0.4924 - accuracy: 0.7464 - val_loss: 0.3436 - val_accuracy: 0.8484
Epoch 2/10
782/782 [==============================] - 5s 6ms/step - loss: 0.2417 - accuracy: 0.9067 - val_loss: 0.3897 - val_accuracy: 0.8292
Epoch 3/10
782/782 [==============================] - 5s 6ms/step - loss: 0.0933 - accuracy: 0.9765 - val_loss: 0.4853 - val_accuracy: 0.8145
Epoch 4/10
782/782 [==============================] - 5s 6ms/step - loss: 0.0227 - accuracy: 0.9968 - val_loss: 0.5251 - val_accuracy: 0.8251
Epoch 5/10
782/782 [==============================] - 5s 6ms/step - loss: 0.0054 - accuracy: 0.9997 - val_loss: 0.5912 - val_accuracy: 0.8254
Epoch 6/10
782/782 [==============================] - 5s 6ms/step - loss: 0.0018 - accuracy: 1.0000 - val_loss: 0.6393 - val_accuracy: 0.8277
Epoch 7/10
782/782 [==============================] - 5s 6ms/step - loss: 8.4706e-04 - accuracy: 1.0000 - val_loss: 0.6729 - val_accuracy: 0.8295
Epoch 8/10
782/782 [==============================] - 5s 6ms/step - loss: 4.7759e-04 - accuracy: 1.0000 - val_loss: 0.7128 - val_accuracy: 0.8288
Epoch 9/10
782/782 [==============================] - 5s 6ms/step - loss: 2.7681e-04 - accuracy: 1.0000 - val_loss: 0.7480 - val_accuracy: 0.8303
Epoch 10/10
782/782 [==============================] - 5s 6ms/step - loss: 1.6451e-04 - accuracy: 1.0000 - val_loss: 0.7848 - val_accuracy: 0.8304
<tensorflow.python.keras.callbacks.History at 0x7f12b69b62b0>