LSTMs

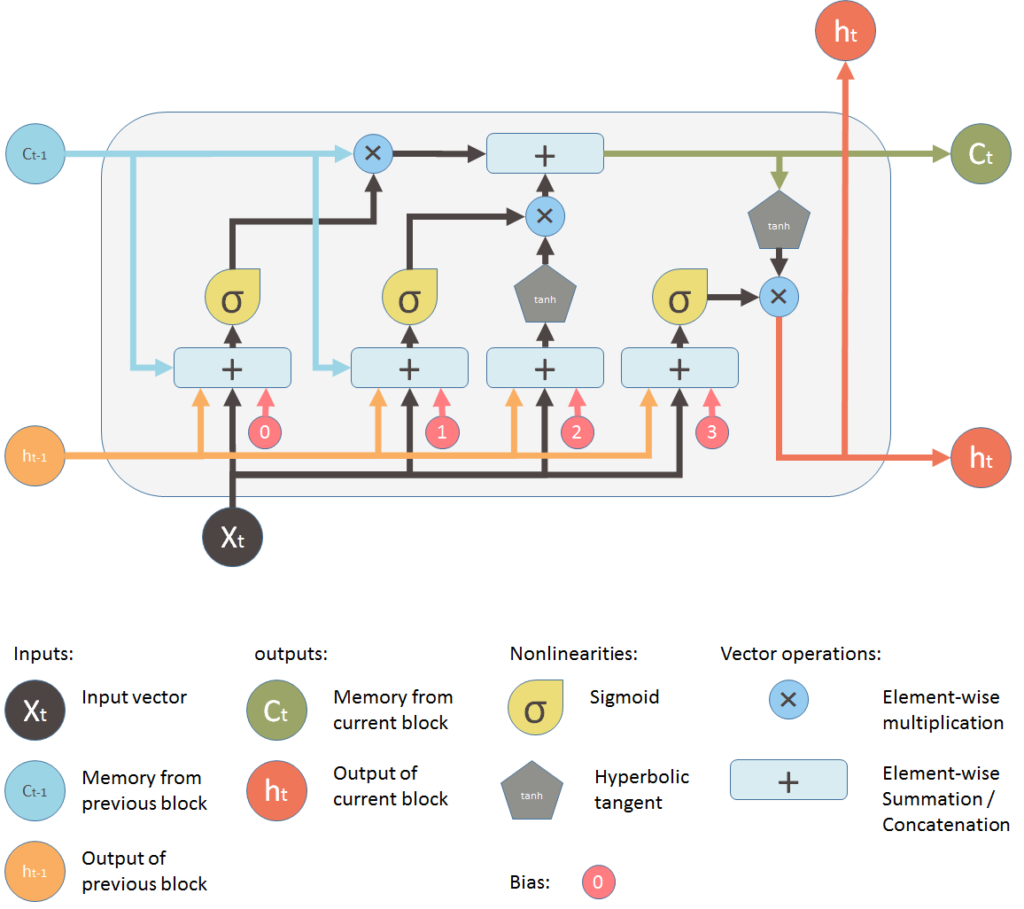
Long Short Term Memory networks – usually just called “LSTMs” – are a special kind of RNN, capable of learning long-term dependencies. They were introduced by Hochreiter & Schmidhuber (1997), and were refined and popularized by many people in following work. They work tremendously well on a large variety of problems, and are now widely used.

http://colah.github.io/posts/2015-08-Understanding-LSTMs/

Pour apprendre LSTM, il y a d’abord cette courte introduction de Laurence Moroney (qui suit une vidéo sur les RNN).

Mais il y a surtout Understanding LSTM and its diagrams de Shi Yan ! avec de très beaux diagrammes et puis en français l’article très drôle LSTM, Intelligence artificielle sur des données chronologiques de Youcef Messaoud.

Enfin il y a Understanding LSTM Networks, de Christopher Olah, citées à juste titre par tous. Bien écrit, clair et « joli » comme d’habitude.

Mais on ne peut pas faire plus clair que le diagramme de Shi Yan.

Prenez le temps de lire tous ces articles pour vous familiariser avec LSTM.

from __future__ import absolute_import, division, print_function, unicode_literals
import tensorflow_datasets as tfds
import tensorflow as tf
print(tf.__version__)

2.2.0

# Get the data
dataset, info = tfds.load('imdb_reviews/subwords8k', with_info=True, as_supervised=True)
train_dataset, test_dataset = dataset['train'], dataset['test']

Downloading and preparing dataset imdb_reviews/subwords8k/1.0.0 (download: 80.23 MiB, generated: Unknown size, total: 80.23 MiB) to /root/tensorflow_datasets/imdb_reviews/subwords8k/1.0.0...
Dl Completed...: 100%
1/1 [00:08<00:00, 8.54s/ url]
Dl Size...: 100%
80/80 [00:08<00:00, 9.41 MiB/s]

tokenizer = info.features['text'].encoder

BUFFER_SIZE = 10000
BATCH_SIZE = 64

train_dataset = train_dataset.shuffle(BUFFER_SIZE)

train_dataset = train_dataset.padded_batch(BATCH_SIZE)
test_dataset = test_dataset.padded_batch(BATCH_SIZE)

On définit un réseau de neurones de type LSTM.

En entrée, on a un Embedding suivi d’un LSTM bi directionnel.

Emdedding est obligatoirement la 1ère couche du réseau.

model = tf.keras.Sequential([
    tf.keras.layers.Embedding(tokenizer.vocab_size, 64),
    tf.keras.layers.Bidirectional(tf.keras.layers.LSTM(64)),
    tf.keras.layers.Dense(64, activation='relu'),
    tf.keras.layers.Dense(1, activation='sigmoid')
])

model.summary()

Le nombre de paramètres en sortie de Embedding est 523840, soit tokenizer.vocab_size (8185) * 64 = 523840

La formule de calcul de nombre de paramètres LSTM est plus compliquée (voir la discussion ici (Number of parameters in an LSTM model)

Le nombre de paramètres est égal à  4(𝑛𝑚+𝑛2+𝑛) et on multiplie par 2 car on est en bidirectionnel. Avec n = 64 et m = 64, alors 4(𝑛𝑚+𝑛2+𝑛)*2 = 66048 paramètres.

Ensuite, avec le réseau Dense, on a 128 (+1 biais) * 64 = 8256 paramètres.

Et pour finir 64 +1 biais = 65 paramètres.

Model: "sequential"
_________________________________________________________________
Layer (type)                 Output Shape              Param #   
=================================================================
embedding (Embedding)        (None, None, 64)          523840    
_________________________________________________________________
bidirectional (Bidirectional (None, 128)               66048     
_________________________________________________________________
dense (Dense)                (None, 64)                8256      
_________________________________________________________________
dense_1 (Dense)              (None, 1)                 65        
=================================================================
Total params: 598,209
Trainable params: 598,209
Non-trainable params: 0

Notez qu’en sortie d’un LSTM on peut en ajouter un autre, à condition de préciser le paramètre return_sequences=True

model.compile(loss='binary_crossentropy', optimizer='adam', metrics=['accuracy'])

NUM_EPOCHS = 10
history = model.fit(train_dataset, epochs=NUM_EPOCHS, validation_data=test_dataset)

Epoch 1/10
391/391 [==============================] - 161s 412ms/step - loss: 0.5154 - accuracy: 0.7362 - val_loss: 0.4047 - val_accuracy: 0.8260
Epoch 2/10
391/391 [==============================] - 162s 414ms/step - loss: 0.4131 - accuracy: 0.8165 - val_loss: 0.5465 - val_accuracy: 0.7552
Epoch 3/10
391/391 [==============================] - 162s 414ms/step - loss: 0.4236 - accuracy: 0.8180 - val_loss: 0.4755 - val_accuracy: 0.8074
Epoch 4/10
391/391 [==============================] - 160s 409ms/step - loss: 0.3084 - accuracy: 0.8798 - val_loss: 0.4615 - val_accuracy: 0.8129
Epoch 5/10
391/391 [==============================] - 160s 410ms/step - loss: 0.2583 - accuracy: 0.9012 - val_loss: 0.4120 - val_accuracy: 0.8406
Epoch 6/10
391/391 [==============================] - 161s 413ms/step - loss: 0.2272 - accuracy: 0.9151 - val_loss: 0.4274 - val_accuracy: 0.8180
Epoch 7/10
391/391 [==============================] - 161s 412ms/step - loss: 0.1860 - accuracy: 0.9339 - val_loss: 0.4379 - val_accuracy: 0.8206
Epoch 8/10
391/391 [==============================] - 161s 411ms/step - loss: 0.1700 - accuracy: 0.9403 - val_loss: 0.5237 - val_accuracy: 0.8362
Epoch 9/10
391/391 [==============================] - 163s 416ms/step - loss: 0.1854 - accuracy: 0.9312 - val_loss: 0.5104 - val_accuracy: 0.8124
Epoch 10/10
391/391 [==============================] - 161s 412ms/step - loss: 0.2955 - accuracy: 0.8712 - val_loss: 0.6128 - val_accuracy: 0.6916