Classification d’iris – #2 – TensorFlow par BackProp

Ce tutoriel de classification d’iris, à l’aide de TensorFlow 2.x est le suivant du … #1 ! au cours duquel nous avons étudié la création du dataset. Tout ce qui est écrit en #1 est donc supposé être connu.

Le problèmeRéférencesCodeGist

Le problème

Classer des iris, en 3 catégories (Iris setosa, Iris virginica et Iris versicolor), à partir des dimensions (largeur et longueur) des sépales et pétales est un problème classique du Machine Learning. Puisqu’on peut le traiter facilement avec les outils de la statistique, pourquoi ne pas essayer de le faire, de façon plus compliquée avec un réseau de neurones ! Tout cela, bien sûr, dans un but pédagogique.

Références

Custom training: walkthrough
Premade Estimators
TensorFlow – tutoriel #1
Tutorial Classification
Scatter Matrices using pandas
How to use Pandas Scatter Matrix
Dataset 5 fleurs
How does the Softmax activation function work?
TensorFlow 2 Tutorial: Get Started in Deep Learning With tf.keras

Code

Le notebook Jupyter, en Python, dans l’environnement GCP est disponible ici.

Gist

Le modèle

Le modèle est un réseau de neurones « classique ». En input 4 neurones pour les longueurs et largeurs des sépales et pétales. En output 3 neurones car il s’agit de classer les iris en 3 catégories (Setosa, Versicolor, Virginica).

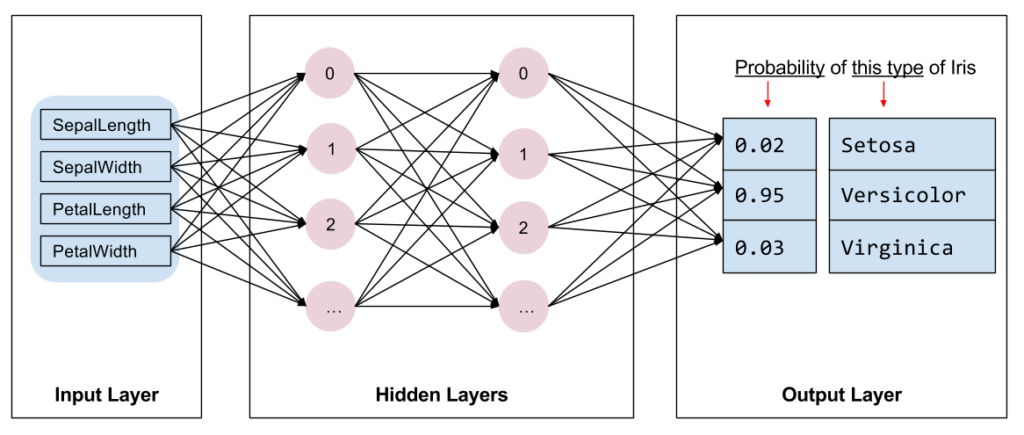
Si on regarde le code un peu plus loin, on constatera que le réseau a 2 couches cachées, chacune ayant 10 neurones. L’activation des couches cachées est de type ReLU, la fonction de coût est SparseCategoricalCrossentropy et l’optimizer est SGD et la métrique accuracy.

Voici ce qu’on aurait codé « normalement »

Aparté – Création du modèle

model_2 = tf.keras.Sequential([
  tf.keras.layers.Dense(10, activation=tf.nn.relu, input_shape=(4,)),  # input shape required
  tf.keras.layers.Dense(10, activation=tf.nn.relu),
  tf.keras.layers.Dense(3, activation=tf.nn.softmax)
])

model_2.compile(optimizer='SGD',
              loss='sparse_categorical_crossentropy',
              metrics=['accuracy'])

model_2.summary()

Model: "sequential"
_________________________________________________________________
Layer (type)                 Output Shape              Param #   
=================================================================
dense (Dense)                (None, 10)                50        
_________________________________________________________________
dense_1 (Dense)              (None, 10)                110       
_________________________________________________________________
dense_2 (Dense)              (None, 3)                 33        
=================================================================
Total params: 193
Trainable params: 193
Non-trainable params: 0
_________________________________________________________________

Pour terminer par un fit.

%%time
history = model_2.fit(train_dataset, epochs=100)

Le code présenté sur le site de tf est différent pour des raisons pédagogiques.

La fonction softmax, l’optimizer, la boucle d’apprentissage sont détaillés plus loin dans ce tutoriel.

Après 100 epochs, l’accuracy est un peu supérieure à 98%

Le modèle

Le modèle créé dans le tutoriel est le suivant :

model = tf.keras.Sequential([
  tf.keras.layers.Dense(10, activation=tf.nn.relu, input_shape=(4,)),  # input shape required
  tf.keras.layers.Dense(10, activation=tf.nn.relu),
  tf.keras.layers.Dense(3)
])

Ce modèle est identique à celui proposé ci-dessus, à une nuance près. Il n’y pas de fonction d’activation sur la couche output. Pas de softmax.

On peut facilement le constater. Il suffit de calculer les prédictions. A gauche, les prédictions du modèle (sans entraînement) avec le modèle du tutoriel, à droite les prédictions du modèle en appliquant un softmax. Dans le 1er cas, on a des logits (valeurs brutes de sortie), à droite on a des probabilités dont la somme par ligne est 1.

predictions = model(features)
predictions[:5]

<tf.Tensor: shape=(5, 3), dtype=float32, numpy=
array([[ 0.6878122 , -1.5320935 ,  0.6060345 ],
       [ 0.9653555 , -1.9105687 ,  0.6736197 ],
       [ 0.37023228, -1.3443916 ,  0.6173678 ],
       [ 0.6115884 , -1.2916659 ,  0.5008637 ],

predictions = model(features)
predictions[:5]

<tf.Tensor: shape=(5, 3), dtype=float32, numpy=
array([[0.5976338 , 0.23491691, 0.16744933],
       [0.5960157 , 0.16433576, 0.2396485 ],
       [0.607449  , 0.2808966 , 0.1116544 ],
       [0.5791178 , 0.23644575, 0.18443651],
       [0.59524715, 0.174331  , 0.23042189]], dtype=float32)>

Appliquons un softmax au 1er cas, pour obtenir des probabilités.

tf.nn.softmax(predictions[:5])

<tf.Tensor: shape=(5, 3), dtype=float32, numpy=
array([[0.4262261 , 0.29656103, 0.27721283],
       [0.42559844, 0.2763909 , 0.2980106 ],
       [0.42909372, 0.30955103, 0.26135528],
       [0.4195043 , 0.29779395, 0.28270176],
       [0.4253938 , 0.27924767, 0.29535854]], dtype=float32)>

Puis un argmax pour obtenir la classe :

print("Prediction: {}".format(tf.argmax(predictions, axis=1)))
print("    Labels: {}".format(labels))

Prediction: [0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0]
    Labels: [1 0 2 1 0 2 0 1 1 2 2 0 0 2 0 1 0 1 1 1 0 2 0 2 1 1 0 2 2 0 2 0]

Les résultats sont évidemment mauvais puisqu’on n’a pas commencé la phase d’apprentissage.

La fonction de perte

La fonction de perte est SparseCategoricalCrossentropy. C’est celle que l’on retient habituellement lorsqu’on est dans le cas d’une classification non binaire et que les données de sortie ne sont pas one hot encoded.

loss_object = tf.keras.losses.SparseCategoricalCrossentropy(from_logits=True)

def loss(model, x, y, training):
  # training=training is needed only if there are layers with different
  # behavior during training versus inference (e.g. Dropout).
  y_ = model(x, training=training)

  return loss_object(y_true=y, y_pred=y_)

l = loss(model, features, labels, training=False)
print("Loss test: {}".format(l))

On calcule le coût sur l’échantillon features.

Loss test: 1.3003196716308594

def pack_features_vector(features, labels):
  """Pack the features into a single array."""
  features = tf.stack(list(features.values()), axis=1)
  return features, labels

train_dataset = train_dataset.map(pack_features_vector)

features, labels = next(iter(train_dataset))
print(features[:5])

tf.Tensor(
[[7.2 3.2 6.  1.8]
 [4.9 3.1 1.5 0.1]
 [5.4 3.7 1.5 0.2]
 [5.  3.5 1.3 0.3]
 [5.5 2.4 3.8 1.1]], shape=(5, 4), dtype=float32)

Au sujet de tf.stack

tf.stack stacks a list of rank-R tensors into one rank-(R+1) tensor.

x = tf.constant([1, 4]) 
y = tf.constant([2, 5]) 
z = tf.constant([3, 6]) 
tf.stack([x, y, z])

<tf.Tensor: shape=(3, 2), dtype=int32, numpy=
array([[1, 4],
       [2, 5],
       [3, 6]], dtype=int32)>

Given a list of length N of tensors of shape (A, B, C); if axis == 0 then the output tensor will have the shape (N, A, B, C). if axis == 1 then the output tensor will have the shape (A, N, B, C)

tf.stack([x, y, z], axis=1)

<tf.Tensor: shape=(2, 3), dtype=int32, numpy=
array([[1, 2, 3],
       [4, 5, 6]], dtype=int32)>

Le gradient

Si on veut de façon explicite, calculer le gradient avec TensorFlow, alors on utilise tf.GradientTape qui permet d’enregistrer les opérations de calcul différentiel.

def grad(model, inputs, targets):
  with tf.GradientTape() as tape:
    loss_value = loss(model, inputs, targets, training=True)
  return loss_value, tape.gradient(loss_value, model.trainable_variables)

Exemple d’utilisation :

x = tf.constant(3.0)
with tf.GradientTape() as g:
  g.watch(x)
  y = x * x
dy_dx = g.gradient(y, x) # Will compute to 6.0

L’optimizer

L’optimizer retenu ici est SGD avec un learning_rate=0.01.

optimizer = tf.keras.optimizers.SGD(learning_rate=0.01)

Il n’y a pas de raison objective à retenir a priori cet optimizer plutôt qu’un autre.

Suite du tutoriel ici.